历表:VSOP87/ELP2000-82
编算:高良超
2025年将有两次月食、两次日食,现分别介绍如下:
一、3月14日 月全食
见食地区
这次月食,在亚洲东部、大洋洲东部、太平洋、北美洲、南美洲、大西洋、欧洲、非洲西部、北冰洋、南极洲部分区域可以看到。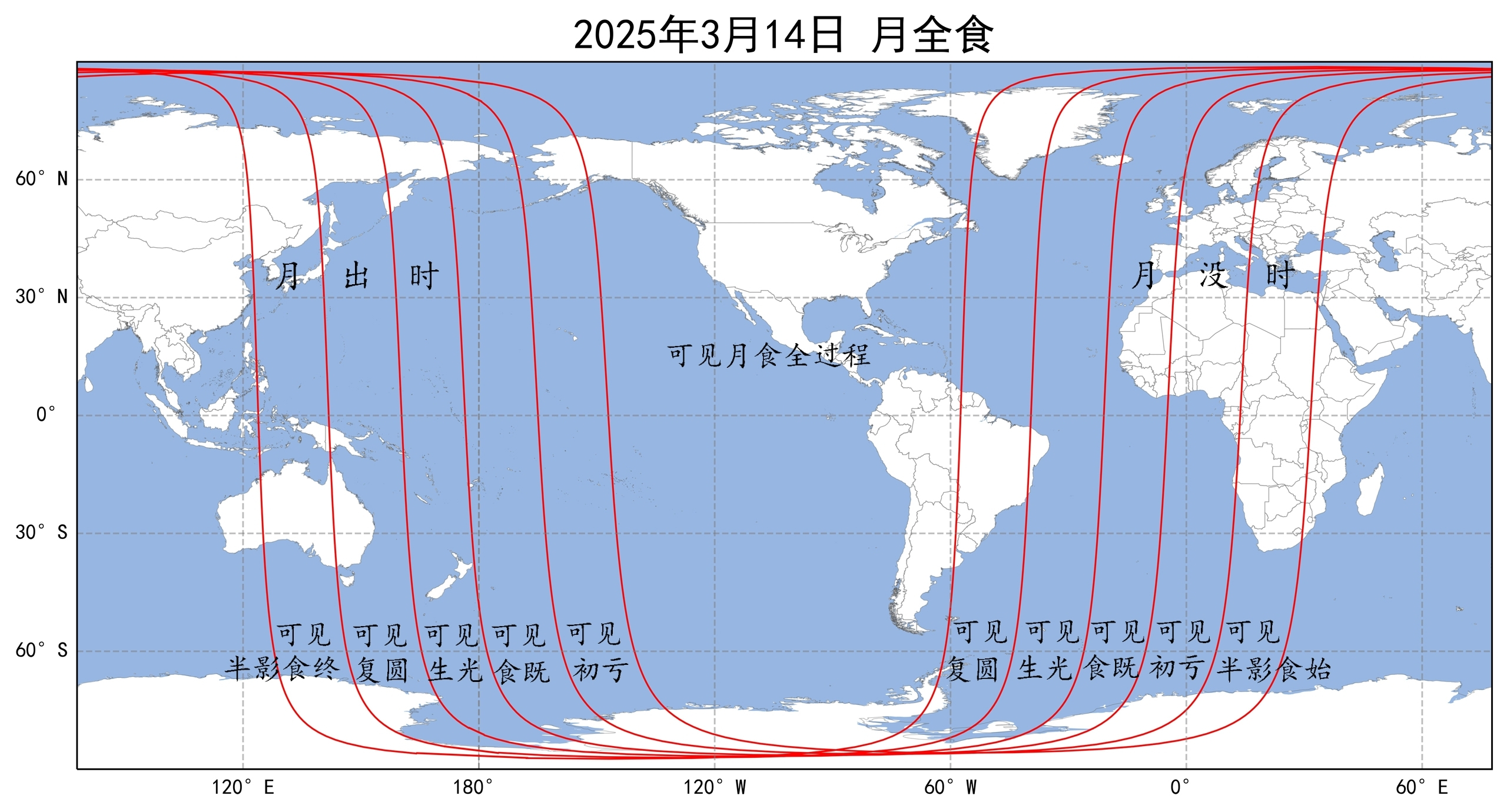
二、3月29日 日偏食
见食地区
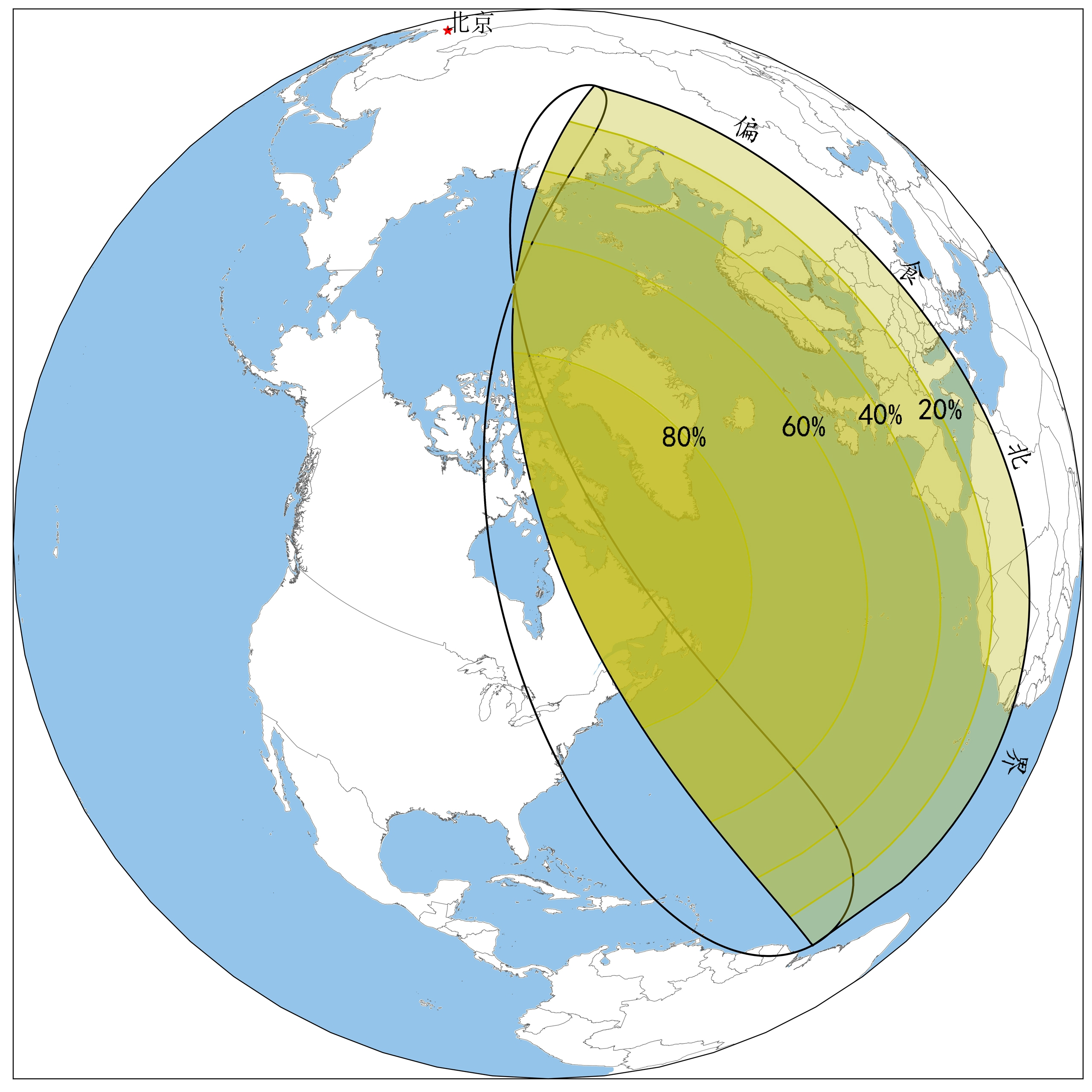
这次日食,在北美洲东北部、南美洲极东北部、大西洋北部、非洲西北部、欧洲(除东南部)、亚洲极西北部、北冰洋部分区域可以看到。
2025年3月29日日偏食概况
太阳和月亮赤经相合时候的力学时:2025年3月29日11h47m25.869s
见食位置
食象 北京时间 地理经度 地理纬度
偏食始 16:50:43 -42°23′ 14°00′
食 甚 18:47:27 -77°13′ 61°16′
偏食终 20:43:46 +90°52′ 72°13′
食分=0.938,γ=1.0405,沙罗序列149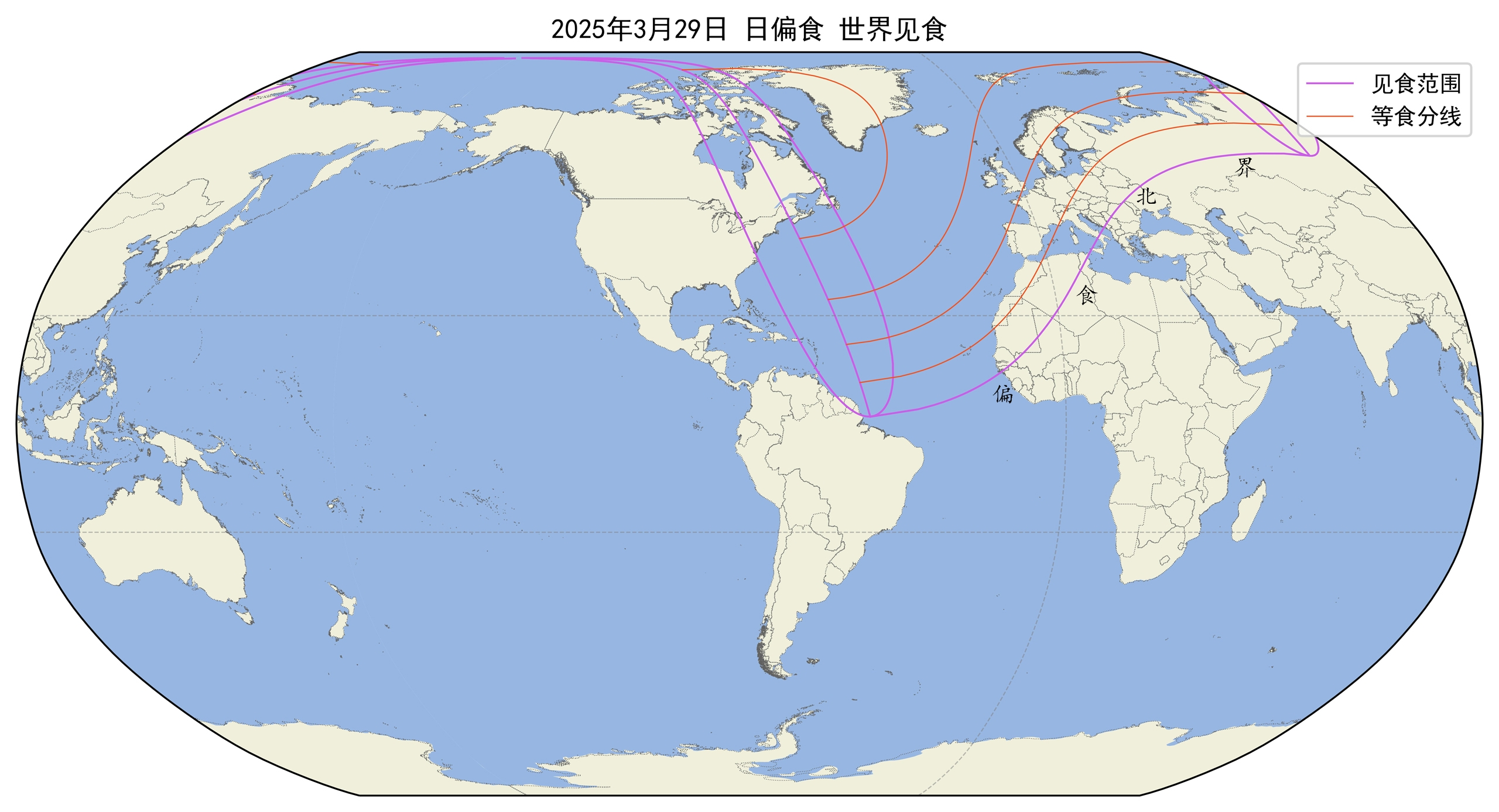
三、9月7~8日 月全食
见食地区
这次月食,在大西洋东部、欧洲、非洲、亚洲、印度洋、大洋洲、太平洋西部、南极洲可以看到。中国全境可见。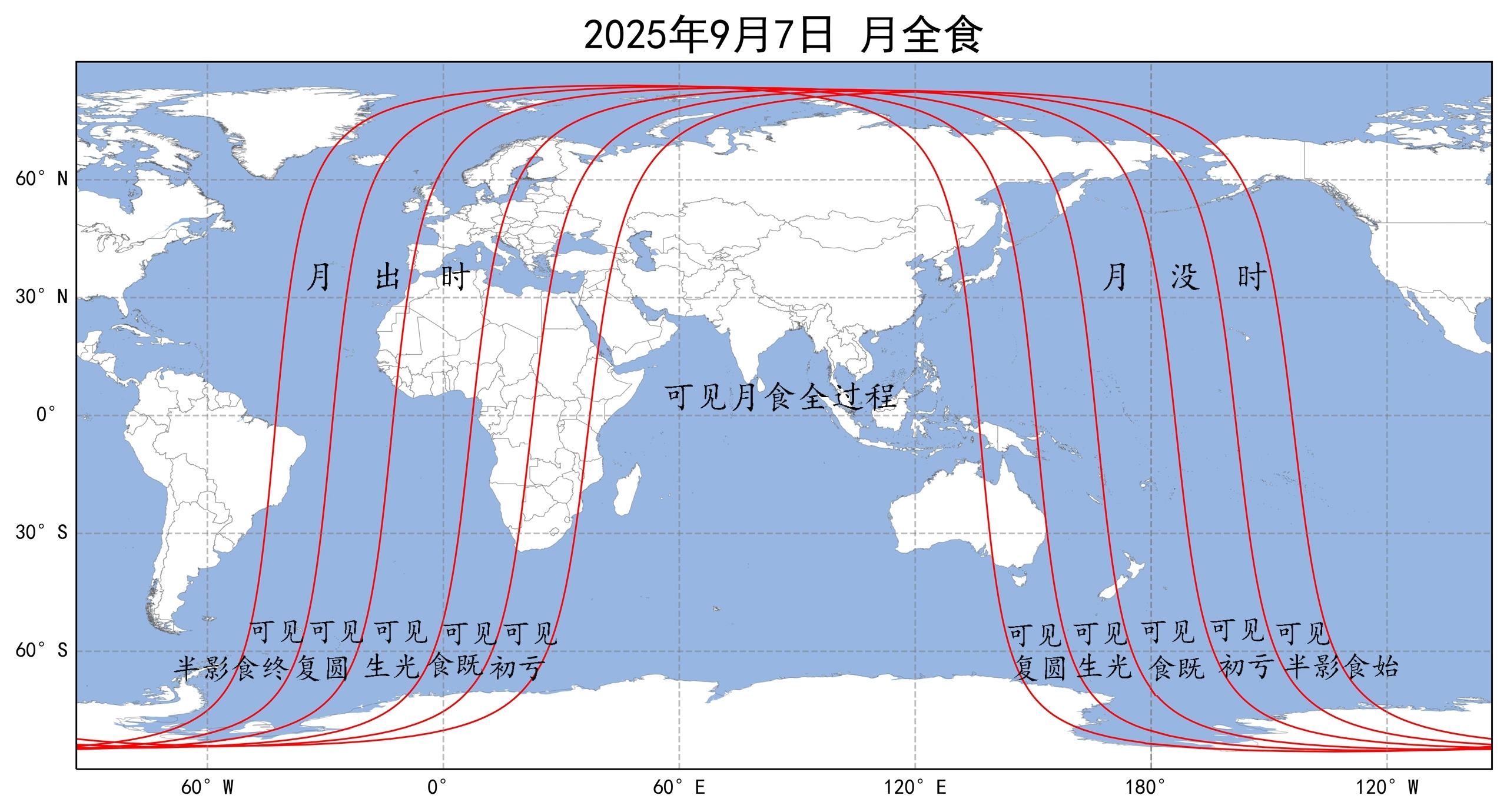

四、9月22日 日偏食
见食地区
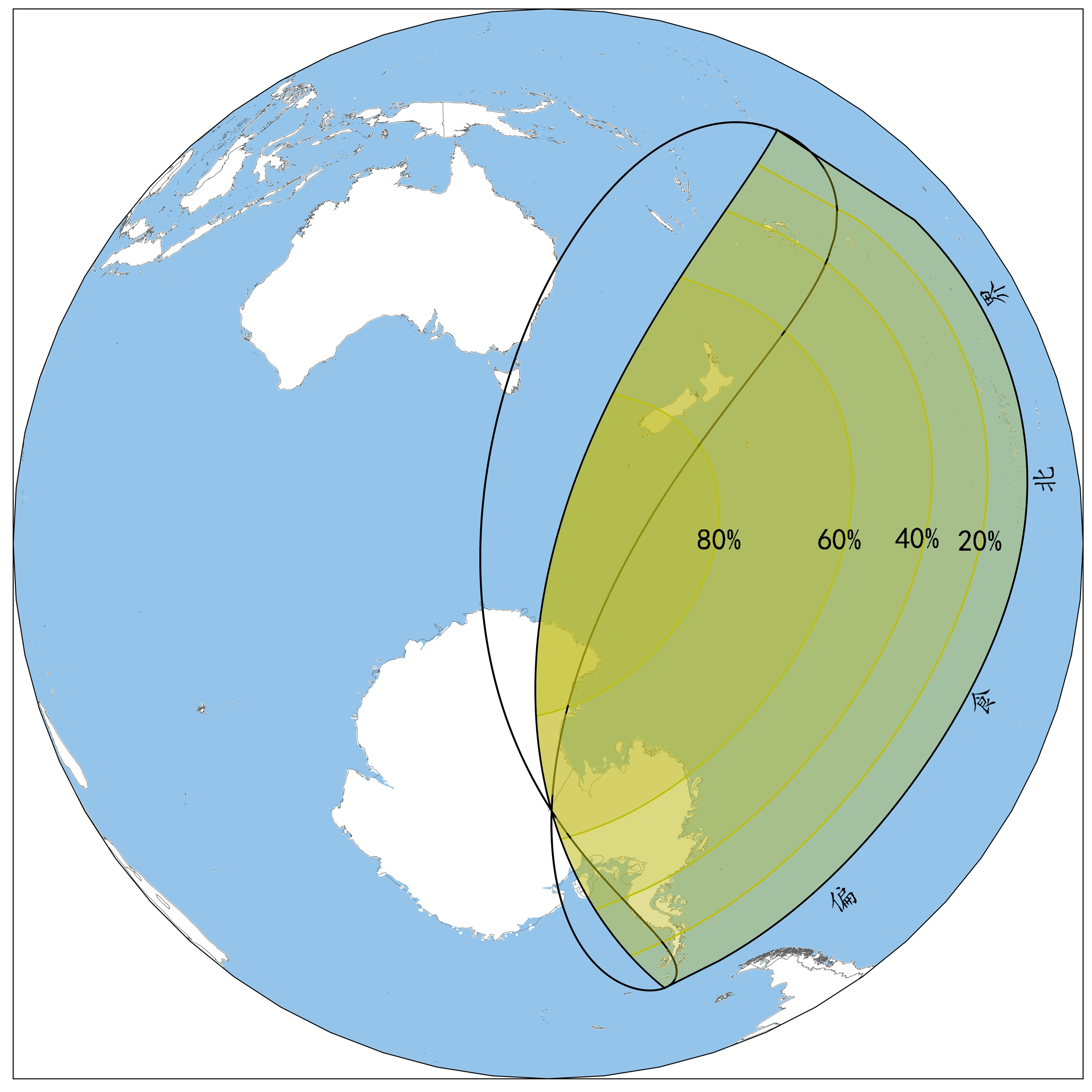
这次日食,在大洋洲东部、太平洋西南部、南极洲部分区域可以看到。
2025年9月22日日偏食概况
太阳和月亮赤经相合时候的力学时:2025年9月21日20h51m37.935s
见食位置
食 象 北京时间 地理经度 地理纬度
偏食始 01:29:42 -174°06′ -13°58′
食 甚 03:41:56 +153°24’ -61°04’
偏食终 05:53:45 -61°17′ -72°16′
食分=0.855,γ=1.0651,沙罗序列154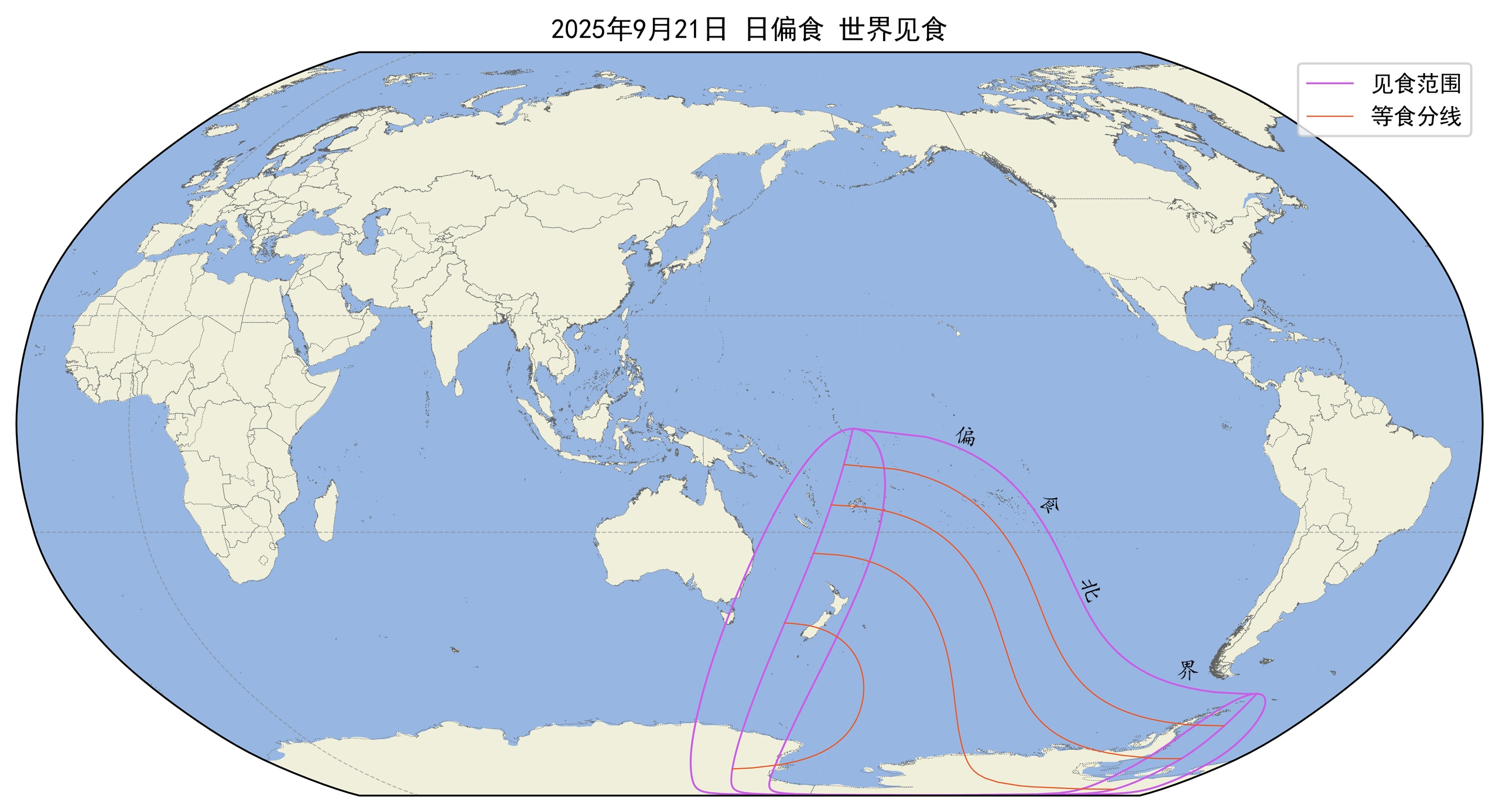
说明
2025年的日月食是根据VSOP87/ELP2000-82历表结合日月食理论计算而来,太阳在单位距离处的视半径值采用959.63″。月亮的视半径根据公式sins月=ksinπ月计算,其中π月为月亮的地平视差,k值取0.272488,为IAU1976推荐数值。太阳和月亮的视半径不包括光渗影响。
本年一共发生两次月食、两次日食,其中9月7~8日的月全食我国全境可见。本年日月食地图使用新版日月食计算软件绘制,由于计算方法的不同,可能会与其他资料值差1~2秒。同时对张雷、宗洋、杨旸、常金龙等同好的大力帮助,在此一并表示感谢。
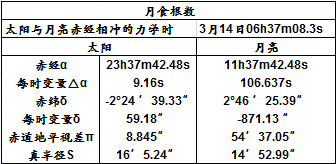
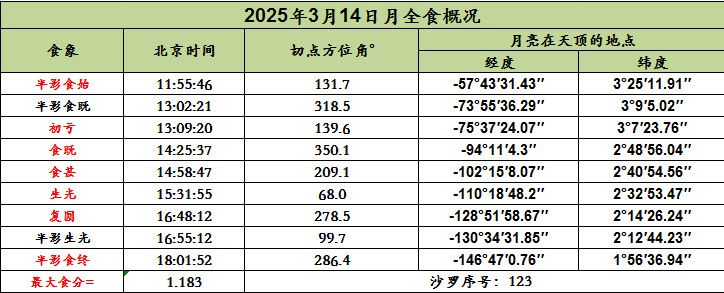
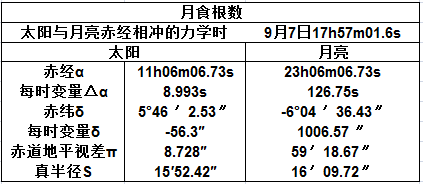
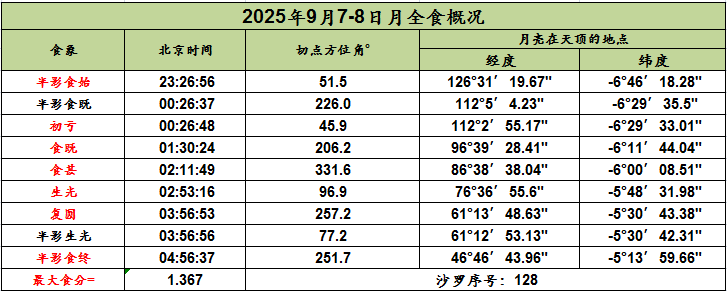
月食概况载半影食始、半影食终及初亏、食既、食甚、生光、复圆时的北京时间。月亮进入地球半影以后,月面光度看不出有显著变化,月亮开始进入本影的瞬刻是偏食的开始,叫做初亏。月亮完全进入本影的瞬刻是全食的开始,叫做食既。月亮中心和地影中心的相距最近的时刻,叫做食甚。月亮开始离开本影的瞬刻是全食的终了,叫做生光。月亮完全离开本影的瞬刻是偏食的终了,叫做复圆。食分(食甚时月亮边缘深入地影的距离和月亮直径之比)。月食时凡能看到月亮在地平线上的地方都可以看到月食,各食象的时间各地所看见的都是一样。
如果要确切地知道某地是否可以看到月食,应先计算该地的月出、月没时刻,再看初亏、复圆间月亮是否在地平线上来决定。
月食概况又载半影食始、初亏、食既、生光、复圆、半影食终时候半影及本影和月亮切点的方位角(从月面正北点向东算起),半影食始、初亏、食既、食甚、生光、复圆、半影食终时地球上见月亮正在天顶的地点的经纬度。
日食概况载日食起迄时刻和见食地点。
偏食始表示月亮半影锥轴初次和地面相切的时刻,就是地面最先看到初亏的时刻,并列出切点的经纬度。
中心食始表示月亮本影锥轴初次和地面相切的时刻,并列出切点的经纬度。
地方视午(或视子夜)的中心食表示太阳和月亮赤经相合的时刻,并列出月影锥轴与地面交点的经纬度。
食甚表示日食食分最大的瞬刻,并列出经纬度。
中心食终表示月亮本影锥最后和地面相切的时刻,并列出切点的经纬度。
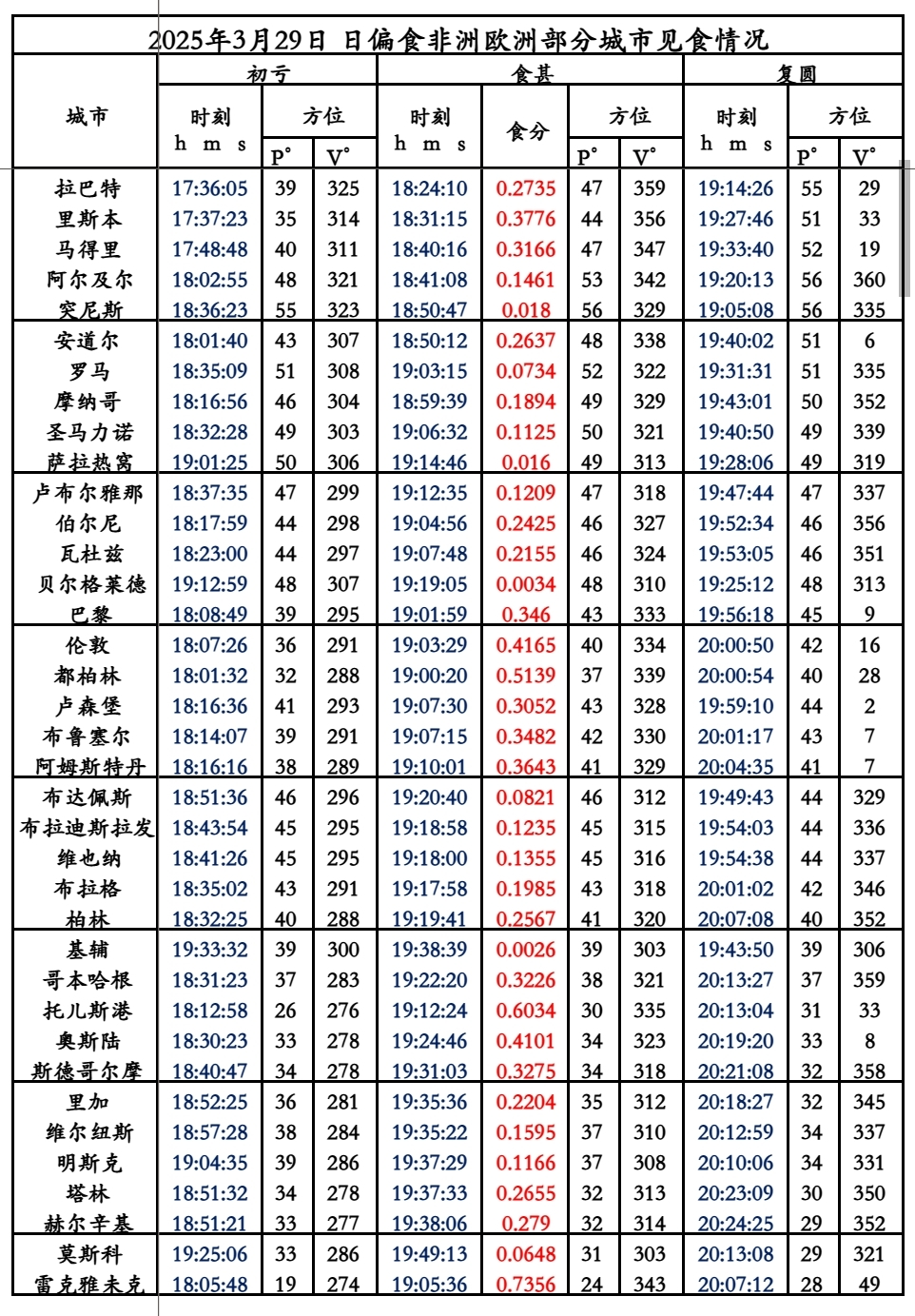
食分(日偏食)某地观测者所看到的太阳被月亮遮盖的分数。食分的大小是日面直径被遮盖部分与日面直径的比值。
偏食终表示月亮半影锥轴最后和地面相切的时刻,并列出切点的经纬度。
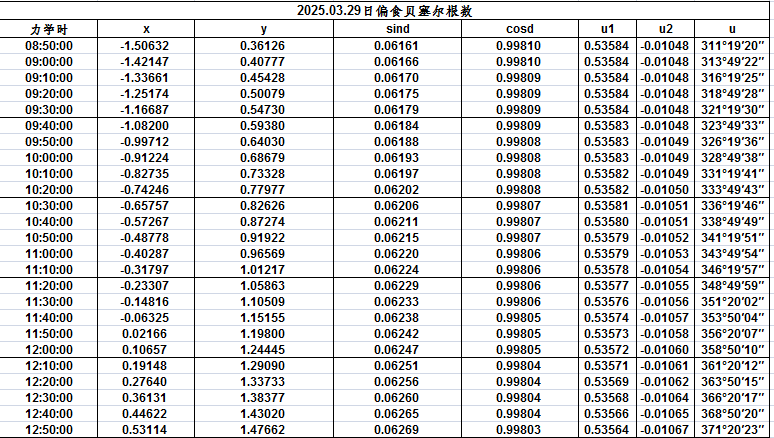
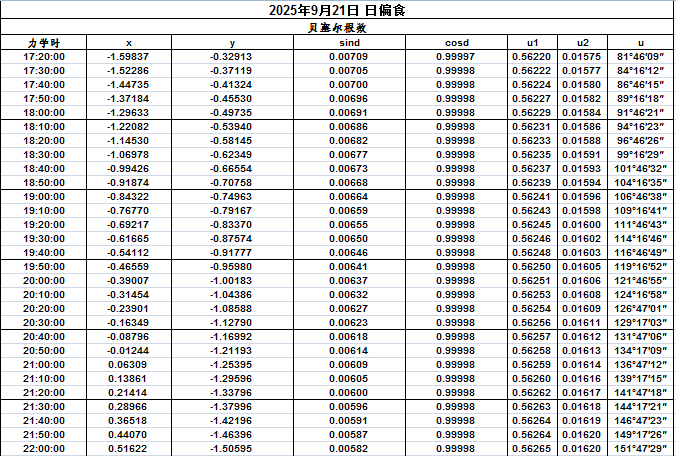
贝塞尔根数供精密计算日食时刻之用,它的几何意义如下:
假设一个平面通过地心,和月影锥轴相垂直,也就是和日月中心的连线相垂直,这平面叫做基本面,以地心为原点,基本面和赤道面的交线为X轴,向东为正。以在基本面上和X轴相垂直的直线为Y轴,向北为正。和基本面相垂直的轴为Z轴,向月亮方向为正。坐标以地球赤道半径为长度单位。
x,y是月影锥轴和基本面交点的坐标。
d,μ是Z轴的方向;d是Z轴和赤道面的交角,μ是Z轴自历书子午圈算起的时角。
u1,u2是半影锥及本影锥在基本面上的半径,以地球赤道半径为长度单位。u1恒为正值,u2和本影锥顶的z坐标同号。本影锥顶在基本面后面时,u2为负值,可以看到全食;本影锥顶在基本面前面时,u2为正值,可以看到环食。在极少数情况下u2在基本面上为正值,而在地面为负值,可以看到全食。
f1,f2是半影锥和本影锥的半顶角。
致谢
(1)本章日食的数据是采用下列文献中的日食公式计算:
Hermann Mucke and Jean Meeus,Canon of Solar Eclipses,-2003 to +2526,Astronomishes BÜro,Vienna,Austria,1983
(2)本章的日食的贝塞尔根数及月食计算是采用下列书籍计算:
Explanatorysupplement to the astronomicalalmanac及《日月食计算》
2025年的天象预报资料,可在“有趣天文奇观”网站下取得,欢迎多加利用!http://interesting-sky.china-vo.org/categories/year/